Dualism vs. Monism — The Mind-Body Relationship

There’s something that’s blindingly obvious, even to those who have never stepped foot in a philosophy class—there are things we see, objects which are seemingly outside of us, and there are things we think, things we cannot pin down to any external location around us.

This is the only realization we need to dive into the great battle between body and mind, the seen and the unseen, the physical and the immaterial.

Diving into the Dual

To dive into the dual the right way, we have to make a pitstop in 600BC Greece. If you’ve taken philosophy in school, this probably sounds familiar (maybe a bit too familiar). But we’re not so much focused on obscure sounding Greekisms like Pythagorean metempsychosis or Pyrrhonistic ataraxia as we are on the exciting elements of the story; don’t you worry.

Around 600 years before Christ, there was something in the water in southern Greece and western Turkey. Humanity has no doubt contemplated its origins since the spawning of self-consciousness many hundreds of thousands of years ago, but this time was different. There was a new, penetrating and insistent sort of musing about the origins of the world which came into vogue.

Thales: An Unusually Reflective Fellow

The most popular rendition of the tale starts with Thales, a man most interested in the origins of the things we see around us. Interestingly enough, as far as we know, Thales was a statesman and engineer—a man of practicality. This is more or less the equivalent of a modern politician, suited up in his sleek coat and pants—with strangely little interest in winning over constituents or scheming for more personal power—sitting down to muse about quantum physics and read some poetry. Yep… this really was a different world!

Thales looked out at all he could see, the expansive night sky above him, and sought an ultimate reason. Why? Why does any of this exist?

But it wasn’t necessarily this inquisitive nature that set Thales apart from those before him. After all, many souls before him had wrestled with the same questions, the same persistent desire to know. What made Thales special was the extent to which he offered evidence for his musings. And although the kind of evidence Thales unearthed might not impress the modern mind, Thales was a pioneer of a method of thought that was about the transform the world around him and long after him.

Perhaps the best way to showcase the brilliance of Thales is through art.

Thales gazed out at the very same world we see around us today. He gazed out at a smattering of shapes, forms and colors.

He observed this world seemingly outside of him and meditated on ways to find some underlying pattern, some underlying reason for which these colorful arrangements exist in the way they do.

Those before him looked up this very same arrangement of objects in the world; they meditated upon the very same questions that Thales did. But there is something Thales did which none before him (as far as we can tell) figured to do. In his careful study of this world of his perception, Thales noticed certain patterns within himself, what we might call mental patterns, and he noticed that these mental patterns themselves followed a certain rhythm.

In other words, Thales recognized that there is some sort of connection between what we see around us and the ways in which we think about these things “out there.” Whereas those before him were content to let that connection between the seen and the unseen pass away in silence, Thales realized that this linkage between patterns of sight and patterns of thought is an extremely important object of meditation and careful study. Talk about a metacognitive leap!

Granted, we love to compare this reflective brilliance of Thales’s to our modern mathematical machinery and scientific skill. And Thales’s ultimate answer, his final reduction of the age-old question, “Why this world?” is rather disappointing considering these shiny new methods of ours—the prime mover of it all, the generator of the cosmos and all else, must be water he confidently claimed.

But the brilliance of his insight—the recognition of the linkage between external and internal patterns—would serve as a springboard for all further musing about the world around us.

Let’s recap what exactly Thales did and dive in a bit deeper now.

Thales looked about the objects around him, gazed up into the stars above, and saw patterns:

And when Thales went to meditate and reflect upon these visual patterns, he noticed patterns of a different sort. He began to notice patterns within his mind, patterns of a non-visual kind. He discovered that these patterns obey basic laws or have certain “habits,” just as the objects around us do. The way that we link ideas and concepts in our mind can be visualized as the creation of roads or maps of reasoning, something like so:

And, as long as we are careful and reflective about our thoughts and ensure that they correspond with the visual patterns around us, we can begin to form some cohesive ideas about those patterns we see around us. In essence, we can begin to form a coherent sort of “image,” informing us of the ingredients of the world we perceive, something like this:

It is this fertile field of contrasting and comparing visual or “physical” patterns with non-visual or “mental” patterns that the battle between body and mind is fought upon.

The composition of the final image (that circle above us)—the smattering of colors and their unique combination—determines which team you root for. If you’re a monist your circle will be monochrome, perhaps a little boring and uninspiring. If you’re a dualist, your circle will be two-colored (and sometimes the “colors” various thinkers use are quite surprising and vivid). And, if you’re exceptionally divergent, what is often called a pluralist, your circle is multi-colored and as diverse as you could creatively conjure up.

Thales was a monist. The conclusion he reached is that all can be reduced to water. His circle might have looked like so:

Entering the Circular Arena

On the topic of circles, we can’t help but broach the iconic Yin and Yang.

In this symbol there is a wealth of philosophical information.

Oftentimes, it is assumed that the yin and the yang—the dark and the light, the passive and the active, respectively—symbolize a sort of rigid dualism. But the story of the yin and yang is much more brilliant than that. In fact, all three of our “teams” of interest—the dualists, the monists and the pluralists—are implicated in the yin and yang.

We said earlier that Thales was the pioneer of a new breed of thought about the world. This is indeed true. But nearly 500 years before Thales, in 1100 B.C. China, arose the pioneers of the crux of our story—the balance between one and many, the battle between dualism and monism.

The I Ching or “Book of Changes” was one of the world’s first works of philosophy. Just as Thales gazed up into the night sky and asked, “Why does any of this exist?,” so did the Ancient Chinese philosophers ponder the very same question.

The I Ching was fundamentally a work of cosmology—its writers sought the ultimate substance or the ultimate principle from which all else took shape. And the answer these fine folks settled on represents an inspiring interplay between mind and matter.

At the very beginning—before time and space themselves!—there was something termed Wuji. The very meaning of Wuji is “without limit.”

Wuji is seen as the circle upon no background. Wuji is that limitless essence or principle, closed in upon itself, with no restrictions placed upon it from anywhere else. Wuji is infinite freedom.

From this rich and fertile Wuji came the initial motion or action of the cosmos—a self fission of limitless potential into an interaction between two halves. After Wuji was Taiji—the “Supreme Ultimate” nature of the cosmos, the division of infinity into the potentials for matter and space and body and mind. 

Taiji ushers in the division between form and content, although it is not yet the actualized, tangible distinction between the visible and the non-visible. Whereas Wuji translated to “without pole” or “without limit,” Taiji translates to “supreme pole” or “grand pole.” Taiji represents the first restriction, the first self-imposed limitation of the limitless freedom of the Wuji.

And it is only after this potential for form and content has been birthed that the yin and yang can spring to life, filling in the boundaries made by Taiji:

In the sense of progression—from the unlimited principle of Wuji, to the alternating dynamic between yin and yang—the I Ching is a marvelous example of dualism from monism. We might say that these ancient philosophers and sages were not quite content to simply choose one “circle,” one composite answer to their questions about the nature of reality. They instead chose three circles, each one intimately connected to the other. 

This brings us to the most natural visualization of the battle between the body and the mind:

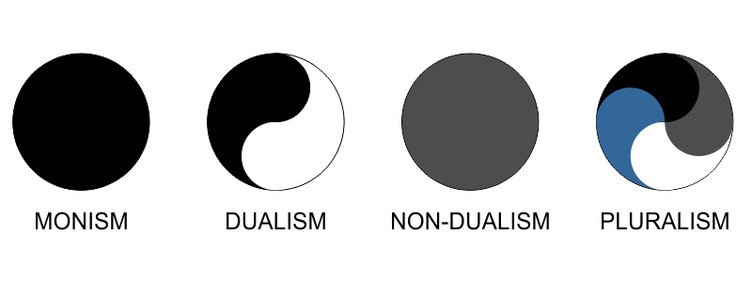
Throughout the rest of our journey, we will survey and sample the various flavors of this smorgasbord. And we will see how these legendary choices can clash in the grandest, most dramatic of ways. But first… we have one more stop to make in Ancient China.

The I Ching and the Birth of Logic

In the age of information and computing technology, we’re accustomed to the fact that logic and logical reasoning are based on 1’s and 0’s, binary code and binary, two-valued operations.

But we might not realize that the basis of this—the alternation between presence and absence, 1 and 0—dates back to 1100 B.C. China, from the very same document we just took a glance at above.

The I Ching didn’t only touch on the general basics of cosmology and philosophy—it also took a deep dive into the specific nature of the various forms that hold our world together. The I Ching document consists of 64 different “hexagrams.” Each hexagram is a figure built from six stacked horizontal lines, where each line is either Yang (an unbroken, or solid line), or Yin (broken, an open line with a gap in the center).

Each one of these hexagrams was a fusion of two separate “trigrams”—a grouping of three lines.

The eight different variations of these trigrams was called the bagua and were held as the fundamental principles or forms of reality:

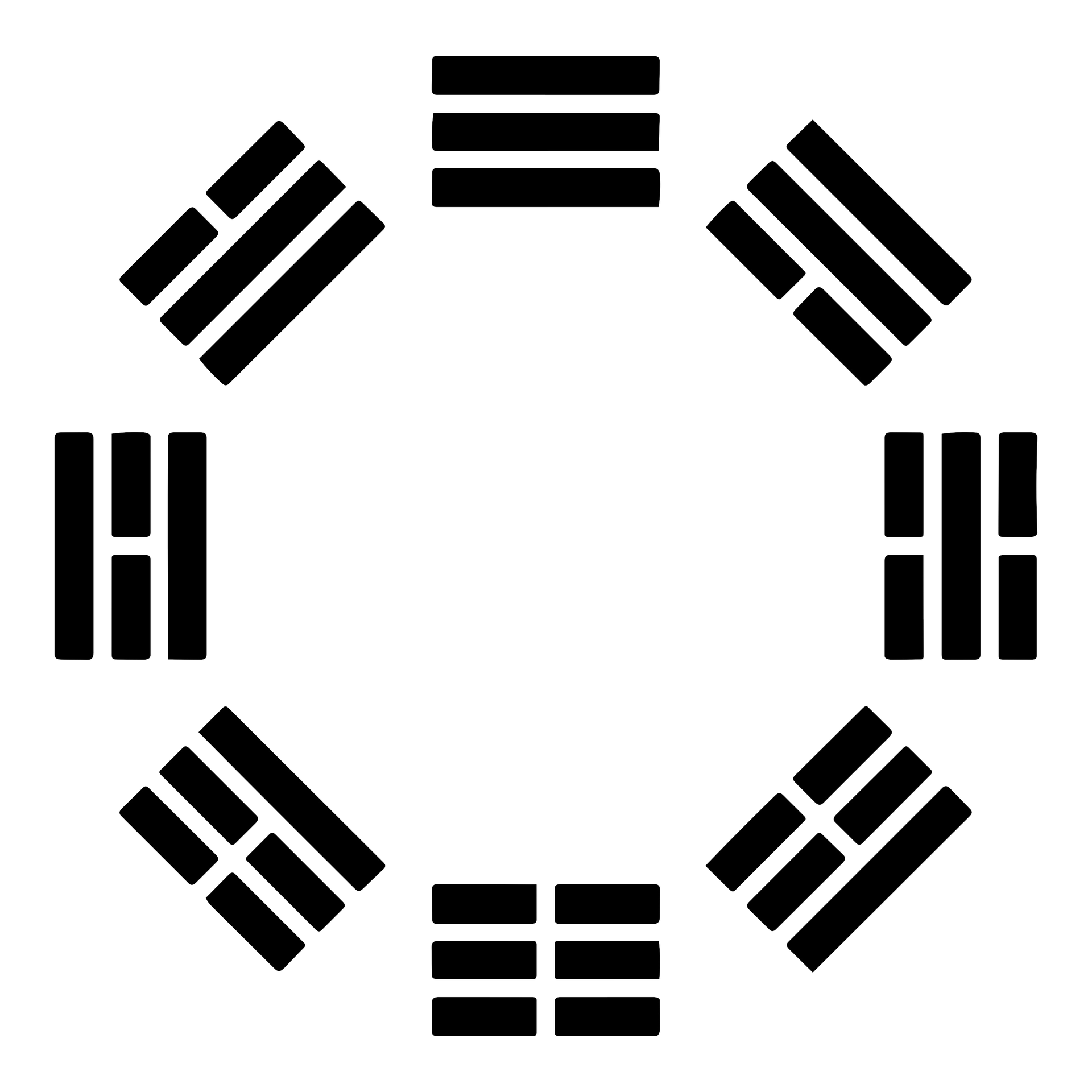
And although these nifty shapes and patterns of lines were drafted up more than a thousand years before Christ—and more than six-hundred years before the philosophers of Ancient Greece!—their overall meaning was anything but dusty or ancient.

These lines—with their duality between solid and split, black and white, presence and absence—are essentially the ancient forerunners of binary code.

“Ok…,” you might say, “That’s cool, but what the heck does this have to do with the ‘battle’ between body and mind?”

To see how these complicated-looking bars relate to our overall journey, we can briefly revisit our old pal Thales.

Remember how Thales looked out at the world around him? Remember how he saw patterns?

And then remember how he also looked within his own mind and saw a different set of patterns? This was a set of patterns that obeyed a different set of rules than the objects he could see around him. This was the world of conceptual and logical paths and connections:

Well… in this light we can liken the I Ching’s groupings of lines to abstract, mental patterns like the ones above. The I Ching recognized the interplay between those two sorts of patterns that Thales recognized. With its vast assortment of hexagrams, the I Ching began to catalog the various forms of abstract patterns that lie behind that which we see around us. The I Ching’s hexagrams centered on the logical, conceptual patterns of the mental world.

And it is these “logical, conceptual patterns” that lead us to the next big figures in the battle between body and mind—the famous duo (and sometimes infamous!) Plato and Aristotle.

Plato’s Forms and High-Powered Dualism

Perhaps the easiest place to start with Plato is inside his “cave.”

Plato was a man of many stories and allegories. And in one of his most famous allegories, “The Cave,” he draws our attention to the flimsy boundary between fact and fiction, between what’s real and what’s not-so-real. 

“The Cave” describes a group of people who, gazing at the shadows of objects upon a wall in front of them, mistake shadows, mere projections, for objects themselves. And although this story has many implications, its core message is this—there is part of the world which we cannot grasp through our senses and part of the world which we can grasp through our senses, and these two parts of the world are fundamentally different. 

Enter Plato’s so-called theory of forms.

Plato essentially attempted to resolve the battle between body and mind by having the mind wrestle the body into submission, so to speak. In Plato’s model of the universe, the abstract and the mental took precedence over the concrete and the physical.

Philosophers since Thales (yes, that dude again) had meditated on the topic of the appearance of objects in the world. They noted the obvious—things change. So naturally, as philosophers, they began to ask what these objects that change really are. Were these changes part and parcel of the nature of these objects, or was such change something else entirely? How did the substance of objects both change and allow the object in question to maintain its structure and its form?

Bertrand Russell in his The History of Western Philosophy, touches in this issue in a down-to-earth way:

Consider a man who loves beautiful things, who makes a point of being present at new tragedies, seeing new pictures, and hearing new music. Such a man is not a philosopher, because he loves only beautiful things, whereas the philosopher loves beauty in itself. The man who only loves beautiful things is dreaming, whereas the man who knows absolute beauty is wide awake. The former has only opinion; the latter has knowledge.

Bertrand Russell

It wasn’t enough for philosophers to simply experience, to see the beauty in front of them. They sought to penetrate beyond the surface layer of the world, beneath the superficial beauties and the appearance of things. The only problem—what in the heck could “beauty in itself” mean. And for that matter, what could anything “in itself” possibly mean? For this, Plato had to dig deep.

The basic logic of Plato’s “theory of forms” goes a little something like this (don’t worry… it’s not quite as crazy as it looks):

1. What is the difference between “knowledge” and “opinion?”
2. She who has knowledge has knowledge of something, because to have knowledge of “no thing” or nothing would be a contradiction
3. Therefore, we know that knowledge cannot be false or wrong in any deep sense
4. But opinions—as opposed to knowledge—can be mistaken. How is this so?
5. Opinions however, just like knowledge, cannot be about “no thing” at all, as this would also be a contradiction
6. But opinions also cannot be fully corresponding to “what is,” or “some thing” as then they would be knowledge and not opinion
7. Therefore, opinions must be of both “some thing” and “no thing.” They must occupy some sort of middle ground between fully existence and non-existence

Having made this distinction between knowledge and opinion, Plato then paired each of these ideas with a part of the world—he paired opinion with the concrete world of the senses, and he paired knowledge with the abstract world of the mind.

To return to Plato’s allegory of the cave, those inside the cave—gazing up at the shadows on the wall—can only have opinions; they are doomed to only grasp the mere appearance of things. Those outside the cave, however (or those who can see the real objects), can be in possession of bona fide knowledge. These “real objects” that are apprehended through the mind are Plato’s forms.

We can now turn to Plato himself:

For each thing that there is, three things are necessary if we are to come by knowledge: first, the name, secondly, the definition, and thirdly, the image. Knowledge itself is a fourth thing, and there is a fifth thing that we have to postulate, which is that which is knowable and truly real.

Plato

Plato goes on to give an example of a circle:

He says about this circle:

There is something called a circle; it has a name, which we have just this minute used. Then there is its definition, a compound of nouns and verbs. We might give ‘The figure whose limit is at every point equidistant from its center’ as the definition of whatever is round, circular, or a circle. Thirdly, there is what we draw, or rub out, or rotate, or cancel. In the fourth place, we have knowledge, understanding, and true opinion on these matters—these, collectively, are in our minds and not in sounds or bodily shapes, and are thus clearly distinct from the circle itself and from the three entities already mentioned.

Plato

He rounds things off a bit mystically, stating—“In each case, anyone who totally fails to grasp the first four things will never fully possess knowledge of the fifth.” But what exactly is this mystical sounding “fifth?”

In fact, this fifth entity is not as mystical or obscure as it sounds. It’s quite easy to see when we set the stage properly.

We might as well go back to our trusty abstract art example…

Recall the world of external patterns:

This is the world of experience, or the world of appearances, as Plato would refer to it. This is where we see the diagram of the circle; this is where we see any sort of definition of that circle that we write down for reference; this is also where we hear the name—“circle.” And, corresponding to Plato’s cave metaphor, this is the world of shadows.

But there is (at least) another half to this story… There is another world altogether:

This is the world of the mind, or the world of knowledge or understanding, as Plato might call it. This is where the idea or concept of the circle resides, and this is where our understanding of that idea or concept lives. This is what exists in the minds of those cave-goers who begin to doubt the reality of the shadows in front of them. These are the burgeoning logical connections that lead those trapped in the cave to those objects outside the cave—those objects in themselves. 

But… and this is a big but… Where are those “objects in themselves” to be located? What sort of world could they possibly inhabit, if they reside fully in neither the world of experience or the mental world?

Plato had a deep and compelling answer.

Just as Thales discovered the linkage between the patterns of experience and the patterns of the mind, Plato hypothesized another linkage.

Plato proposed a linkage between the logically governed world of the mind and a logically governed world of forms or essences. And these forms could be said to reside in the mind of reality itself, some sort of higher mind or higher realm than the mere human mind.

When our mind contemplates the idea of a circle, it taps into another world altogether—the mind interfaces with the world of Ideas or the world of Form. Whereas the mental world below can weave together ideas and concepts, many of these ideas are to some degree polluted or impure versions of the perfectly whole and perfectly symmetrical Ideas which embody the timeless nature of each concept and each object.

Thus, in the case of the circle, we might envision the world of form which embodies “circleness” or the essence of all circles as something like so:

Whenever we draw a circle or define its characteristics, we are able to do so only because of the connection of this higher, Platonic realm with the worlds of experience and mind. This connection runs to the mind and then to the external world of experience:

This is where Plato’s forms meet his theory of reality, his metaphysics.

But unfortunately, we must travel on. We’ve taken what we’ve needed from our pal Plato. And now it’s time to drop in on his slightly younger, yet no less brilliant, compatriot—Aristotle. What we’re particularly interested in is not Aristotle’s Ethics, nor his Politics or Poetics. Rather, we’re interested in the new breed of science he single-handedly invented—the science of logic.

Aristotle’s Science of the Mind

Just in case you haven’t seen enough circles:

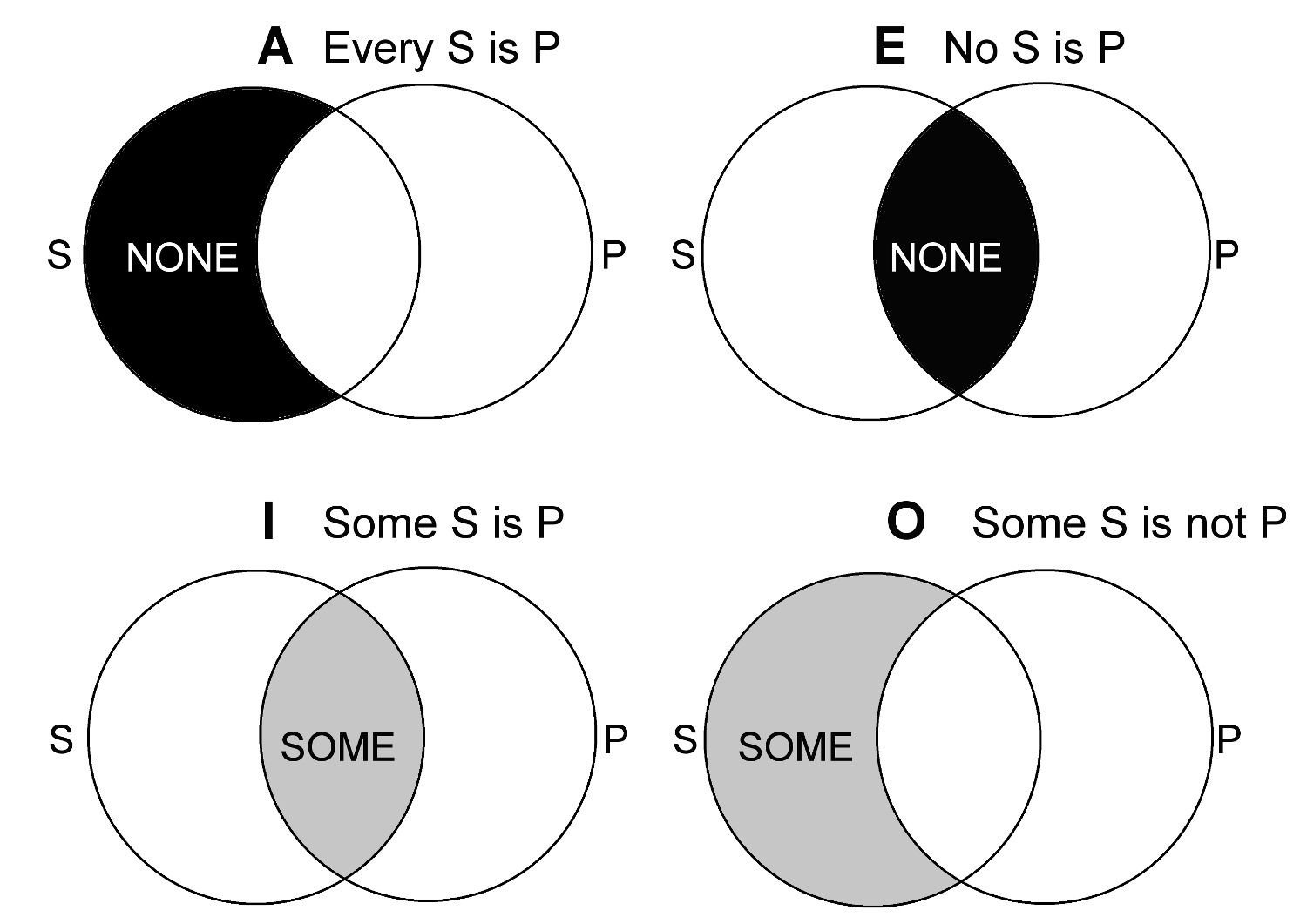
This is perhaps the most iconic representation of Aristotle’s new breed of science. These sorts of patterns of inclusion and adjacency are referred to as a whole as “syllogisms” or “syllogistic logic.” And this portion of Aristotle’s thought is often simply—if not a little carelessly—referred to as the “study of the correctness of reasoning.”

But the truth of the matter—the depth of the story—is far more interesting.

Aristotle titled his collection of works on logic “Organon.” Organon means tool. Aristotle didn’t see his science of logic as a brittle or pedantic study of reasoning or arguments. Rather, he believed logic was a tool of all tools. He believed that logic comprised the tools of thinking that all sciences use. The study of logic was therefore the study of the process of scientific inquiry itself. It was a study of the mind and its relationship to reality.

We see this mental nature of Aristotle’s logic in his chapter of the “Organon” on language, thought and truth. He claims here that “Spoken words are the symbols of mental experience and written words are the symbols of spoken words.” And he goes on to assert that, “Just as all men have not the same writing, so all men have not the same speech sounds, but the mental experiences, which these directly symbolize, are the same for all, as also are those things of which our experiences are the images.”

And herein lies his great step up from Plato—whereas Plato explained the external world through means of some sort of “ideal” world whose dynamics we are not fully privy to, Aristotle devised a means of examining the dynamics that occur between the external world and our mental worlds in exciting depth.

Aristotle devised a science to abstract over all possible forms of reasoning.

We might as well put things pictorially once more to hammer the point home… Plato’s map of reality looked something like this:

There is the external world of perceptions on the left, the internal world of the mind in the middle and the “ideal” world of the forms on the right.

But it was never quite clear how exactly this “ideal” world operated, how exactly it interacted with the other two worlds “below” it.

Aristotle ditched the assumption of this ideal world and decided to focus on this relationship:

He asked himself what sort of things we can expect from this dynamic interaction between the observable and the non-observable, the concrete and the abstract.

And he deftly crafted a breed of science which describes the boundaries of this relationship with stunning precision.

Aristotle’s logic serves as the springboard upon which all subsequent rational investigation of reality must leap (whether or not they explicitly mention or realize this).

And although there is much befuddlement and confusion made of this part of his work, the gist is quite simple. All we need to show the spirit of Aristotle’s logic are four easy graphics. The crux of Aristotle’s science is predication, the assignment of attributes to objects:

These different types of predication can be conveniently abbreviated like so:

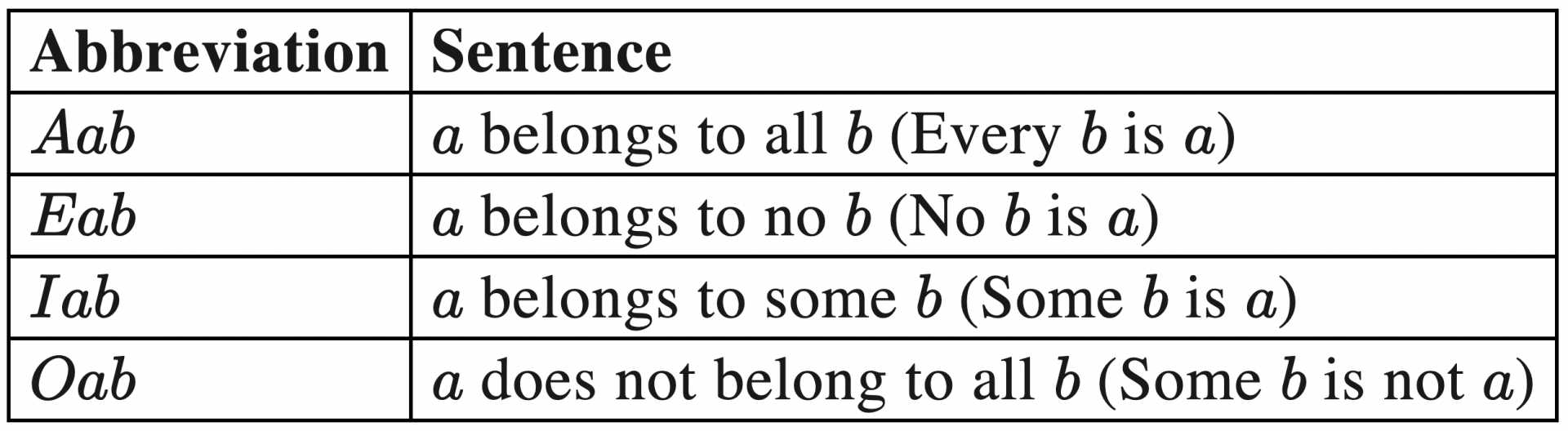
Each of these abbreviations—Aab, Eab, Iab and Oab—can serve as either a “premise” or a “conclusion.” A string of premises that lead to a conclusion constitutes an “argument.” Each of these abbreviations can also be “asserted” to be either true or false. This is somewhat redolent of the trigrams from the I Ching that we explored earlier. Both deal in the patterns of presence and absence.

An example of a true sentence of the form “Eab” could be something like: “No person has three hearts.” In this example, the property of having three hearts is predicated on the subject “people” or “persons.”

Moving on from these, Aristotle then derived the properties of reasoning by employing what he calls “conversions” and “inferences,” specific movements between each of the abbreviated terms above— Aab, Eab, Iab and Oab. Conversions are simply translations between abbreviations. For instance, Eab is equivalent to Eba. To use the same example as above, “No person has three hearts.” is the same as “Nothing with three hearts is a person.” Aristotle listed three such “conversions”.

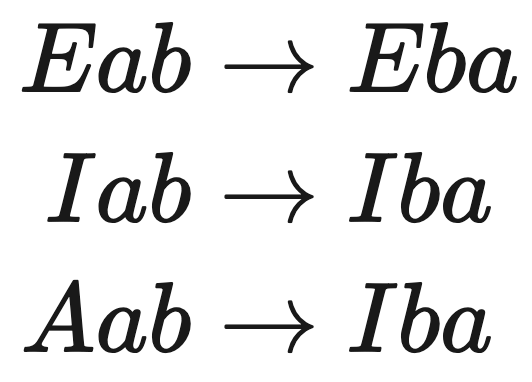
Finally, we have inferences. Aristotle singled out 14 different inferences that hold true regardless of the content of the objects or the nature of the predicates/properties attached to them. This is an example of one of these inferences:

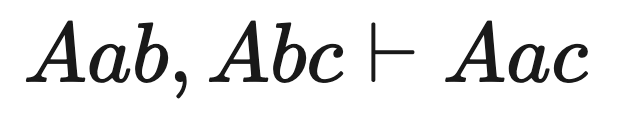
Admittedly, these sorts of things can be extremely dry and brittle, but the overarching idea behind Aristotle’s logic is quite exciting. Each of these structural twists and turns is part and parcel of the rich and colorful tapestry that is the patterns and operations of our mental world:

It is these various twists, turns and connections that allow us to acquire knowledge from the world around us. It is this structure which affords us the ability to know anything at all.

Moreover, it is this invention of Aristotle that leads us into the next round of the great battle between body and mind—rationalism vs. empiricism.

Rationalism vs. Empiricism: How Do We Win Our Knowledge?

Rationalism and empiricism are two terms that are tossed around a lot in philosophy class. But what are they? And more importantly, can they be understood in straightforward and commonsense terms?

Perhaps the easiest way to explain the pair is to remember Aristotle’s “Organon” and his reasons for calling it that. Remember that Organon means “tool,” and Aristotle saw his new science as the best possible tool to reason about how the mind comes to knowledge and certainty.

But this tool of his was only a structural tool. In a sense, his logic was a skeleton upon which the meat and substance of knowledge would come to sit. But this skeleton could only be used to test the validity of thinking, once the facts about the world were collected. The question of how exactly one should go about furnishing said skeleton with substance remained an unresolved question. This is where rationalism and empiricism enter the ring.

The gist is extremely straightforward:

Rationalists believe that knowledge can be secured through our minds and their power of reason alone. They tend to be highly skeptical of any sort of information or seeming facts taken in by the senses. Empiricists, on the other hand, believe that the mind—that ever-invisible friend of ours—cannot be trusted. They tend to trust in what can be sensed and perceived.

This much is straightforward. But here’s where things get a little… weird.

Rationalism and empiricism respectively are not innately coupled with dualism or monism. One can be a rationalistic dualist, an empiricist monist, a rationalistic monist or an empiricist dualist. And you’ll find these terms and their intersections bandied about from paper to paper, in philosophy journals all across the world.

But let’s keep things digestible and clean.

Let’s stop talking about rationalism and dualism themselves and visit another one of philosophy’s heroes. This time, we must travel to 17^th-century France.

Descartes’ Dualism: The Rationalism of René

With the rise of the “dark academia” aesthetic—with its towering Gothic libraries and dark mahogany studies—Descartes and his drawings have become even more popular than before. Descartes certainly had a certain “edge” to him, and his work reflects this contrarian, somewhat irreverent style.

Descartes is a textbook rationalistic dualist, and the entire weight of his towering conclusions rests upon this approach. But the means by which he reached this approach are quite interesting, nearly as mystical, Gothic-tinged and legend-inciting as the man himself.

Legend has it (and so does his most trusted biographer…) that something strange happened to Descartes on St. Martin’s Day or “Old Halloween” of 1619. Descartes was a member of the Dutch army and was stationed in “Neuburg an der Donau” in southern Germany. It was a night of howling wind and bitter cold and Descartes had just shut himself in for the night in a tiny room with a cocklestove. After he fell asleep that night, he had a series of three dreams. Upon waking, he was armed with new knowledge, as if by magic. And for years after this occasion, he insisted that he was visited by some sort of “divine spirit”—whether this was an angel or a demon was never ascertained—who bestowed this knowledge upon him.  After he left that tiny, stove-heated room, he had formulated analytic geometry and had a vision for a brand new philosophy of science. This philosophy was founded upon one core principle, one undeniable truth—the infamous “I think, therefore I am.”

Descartes was alive in a time that had begun to blossom with a zeal for knowledge. The mysticism, esotericism and religion of the centuries past had lost much of its luster for the brightest minds, and they were eager to dig to the bottom of the reality beneath their feet. Those very same questions asked by the I Ching, Thales, Plato and Aristotle—Why does this world exist?, How can we know anything for certain?—returned. They returned with a vengeance not yet seen. 

Descartes was no pasty, sheltered nerd in any deep sense either. He was a worldly man, a man who collected many experiences and lived a full life. In his own words:

I entirely abandoned the study of letters. Resolving to seek no knowledge other than that of which could be found in myself or else in the great book of the world, I spent the rest of my youth traveling, visiting courts and armies, mixing with people of diverse temperaments and ranks, gathering various experiences, testing myself in the situations which fortune offered me, and at all times reflecting upon whatever came my way to derive some profit from it.

René Descartes

He brought this inclination to bear on his approach to philosophical inquiry. He was not content to simply build upon the arguments of others or to immerse himself in books written before him. Descartes sought, with a fervently independent spirit, to settle as deeply as possible into philosophic truth. And in his most famous work of philosophy, Meditations on First Philosophy, he launched a full-scale attack on all which can be doubted. A plan equally as strange sounding as it was ambitious—Descartes plotted to doubt more than any human had before. The final question being, is there anything in this world which cannot be doubted?

Descartes prepared himself to undergo a great journey through mental space, as he weaved his way through the lead-up to the meat of his Meditations. Once he got down to business, he made things quite clear, stating his mission—“If you would be a real seeker after truth, it is necessary that at least once in your life you doubt, as far as possible, all things.” And then he launched, diving deeply into the nature of reality, knowledge and doubt:

I suppose therefore that all things I see are illusions; I believe that nothing has ever existed of everything my lying memory tells me. I think I have no senses. I believe that body, shape, extension, motion, location are functions. What is there then that can be taken as true? Perhaps only this one thing, that nothing at all is certain.

René Descartes

Along this line of inquiry, Descartes fashioned a literary aid—an “evil demon” which had the power to deceive one’s senses, to fool one into thinking things real which are merely illusions.

The more deeply Descartes settled down into the seas of doubt, the darker things grew. He found that he could doubt… well… seemingly everything. But he noticed something interesting as he attempted to doubt—in one fell swoop—all possible things. He noticed that his own mind, his own thinking process itself had a special property: 

I decided to feign that everything that had entered my mind hitherto was no more true than the illusions of dreams. But immediately upon this I noticed that while I was trying to think everything false, it must needs be that I, who was thinking this, was something. And observing that this truth, “I am thinking, therefore I exist” was so solid and secure that the most extravagant suppositions of sceptics could not overthrow it, I judged that I need not scruple to accept it as the first principle of philosophy that I was seeking.

René Descartes

It was there that Descartes reached the bedrock he had been so ardently seeking. But this was by no means the end of things (how could it be with such a mind as Descartes?). There were still two very important questions however—(i) what does this mean about the nature of reality? and (ii) how can we know that this “bedrock” is the actual truth?

Descartes’ answer to the first question hammers home his dualism, while his answer to the second is the centerpiece of his system of rationalism.

Regarding the former point, Descartes reasoned that, on the contrary, if he were somehow not thinking, then he would have no reason to believe that he even existed. Thus, the thinking being must be some sort of substance whose whole essence is to think. The fact that this “thinking thing” is encased by a seemingly physical body is therefore of little importance; it is the mind that matters.

This is the origination of the breed of dualism known as Cartesian dualism. This form of dualism is perhaps the most extreme of all dualisms.

And although Descartes ambitions were grand, he had a great deal of trouble explaining how exactly it is that the so-called mental substance and the physical substance interacted with each other. In other words, if the mind is really so different than matter, what serves as the “glue” to hold them together?

Descartes had a radical (and, on the whole, radically disappointing) answer:

He held that the correspondence between mind and body took place in the pineal gland, deep in the human brain, hence the origin of this dark-academia-style graphic. But beyond conjuring up a physically precise location where this correspondence between mind and body supposedly took place, Descartes was unable to fashion a coherent answer as to how any of this worked.

This brings us to Descartes’ rationalism, the rationalism built upon the question—how can we know that the “I think, therefore I am” conclusion is the actual truth?

To Descartes, the truth of the fact that he was thinking was ensured because of this idea’s clearness and distinctness. In other words, the fact that Descartes was thinking was a logically self-evident truth. The idea was “clear” to Descartes in the same sense that one’s visual perception of their hands in front of them while fully alert and aware; an idea is “clear” when it is in sharp intellectual focus. And the idea was “distinct” to Descartes in a more specific sense. He considered an idea to be distinct when—in addition to being clear or sharp in intellectual focus—all other ideas not belonging to it are completely excluded from it. In other words, when one is thinking, one is not also not thinking. When one has a clear perception of a chair in front of them, one is not also seeing the absence of a chair in front of them.

Via this method of establishing self-evident truths upon clarity and distinctness, Descartes was able to fasten down his dualism in a logically tight fashion: 

[O]n the one hand I have a clear and distinct idea of myself, in so far as I am simply a thinking, non-extended thing [that is, a mind], and on the other hand I have a distinct idea of body, in so far as this is simply an extended, non-thinking thing. And accordingly, it is certain that I am really distinct from my body, and can exist without it (AT VII 78: CSM II 54).

René Descartes

Although this method of Descartes’ seems a bit tame today, it is interesting to consider his rationalism as a precursor to 20^th-century philosophy of mathematics and logical philosophy, in the manner of such giants as Ludwig Wittgenstein, Bertrand Russell and Gottlob Frege (the first of whom we’ll visit shortly).

Descartes’ “clearness” requirement roughly corresponds to the requirement that mathematical axioms be self-evident (or at least appear that way!). And his “distinctness” criterion corresponds to the necessity of non-contradictory statements; every mathematical statement or proof must not occur in conjunction with its negation. Interestingly enough, it is this rationalism of Descartes that morphed into a high-powered “logical empiricism” come the early 20th century, but we’ll get to that later!

All in all, Descartes represents perhaps the first philosopher since Aristotle to step outside the intellectual bubble of his contemporaries and rely upon the prowess of his own mind and that mind only. And although much of Descartes’ philosophy is now seen as a bit antiquated, his rationalistic contribution to philosophical method was a tremendous one.

But not all rationalistic roads lead to Cartesian dualism. In fact, not all rationalistic roads lead to dualism at all… Our next stop lies on yet another rationalistic road. But this time it leads to someplace else, a mighty monism and the accompanying beauty that comes along with monistic unification. Next stop—Leibniz.

Leibniz’s Logical Monism: Rationalism Re-Tooled

We’re told that a teenage Leibniz could be found hiking through the German countryside, balancing upon the rocks beneath him and balancing in his head the merits of Aristotelian philosophy and Cartesian philosophy. Gottfried Wilhelm Leibniz was born an even fifty years after Descartes, in a city only several hundred miles away. Intellectually speaking, he had Descartes’ hefty shoulders to stand upon.

It had also been evident that Leibniz was special since he was young.

At the age of nineteen he published a logical treatise, De Arte Combinatoria, which not only investigated Aristotle’s logic but launched an inquiry into a new and exciting idea of the time—the notion that there is an “alphabet of human thought.”

This idea posited that, in theory, all concepts we use in our thinking can be broken down into a relatively small number of “simple” concepts, concepts which can be reduced no further. And it is these so-called simple concepts which serve as the “alphabet” or building blocks of all human reasoning. This is a similar project to that of Aristotle’s logic. Only this time, Leibniz and his contemporaries sought to build a comprehensive “catalog” from which all possible truths could be assembled. This “catalog” of the alphabet of the mind would serve as a sort of guide or instruction manual for scholars; it would guide their investigations and help to grease their mental wheels.

And, oh yeah… the “concept art” Leibniz came up with wasn’t so shabby either:

But although this early portion of Leibniz’s thought is extremely interesting, it is his later work, his work on the nature of reality and metaphysics that we are most interested in. Much like Descartes, Leibniz was both a mathematician and a philosopher, and he brought his mathematical acumen to bear on his philosophical thought, fashioning a rationalistic view of reality that gave Descartes’ a run for his money.

Much noise has been made in recent years about reality being some sort of “simulation,” or some sort of illusion. And interestingly enough, Leibniz was the forerunner of this way of thinking. In 1714, Leibniz published his best known work—The Monadology. This work dives into many thrilling and puzzling concepts that we are still wrestling with today.

But before we see The Monadology in its full scope, we should take a mini field trip back to the modern day.

One of the words and concepts that transfixed Leibniz and was featured prominently in The Monadology is “automata.” Today we have an entire field of study dedicated to this concept, and the weight of several centuries worth of logical, mathematical and philosophical development are behind it.

One of the most inspiring examples of such “automata” in action is that of John Conway’s “Game of Life.”

In 1970 the British mathematician John Horton Conway devised a sort of mathematical game with extremely simple rules yet extremely fascinating, often wildly unexpected results. This so-called Game of Life consists of a large grid tiled with square boxes or cells.

Each of these cells has two possible states, on or off, colored or non-colored. For each cell, a set of cells called its neighborhood is defined relative to the specified cell. Then, just as time is the parameter along which objects move around us in the physical world, this tiled grid of cells was also given a time parameter. An initial state or arrangement of the entire grid was selected by assigning a state (on or off) to each cell of the grid. This initial state was often simply called (t = 0).

Then… the starting gun goes off.

The initial state of t = 0 becomes t = 1 as each state of each cell on the grid is mapped or transitioned into a new state. And as this process continues on, from t = 1 to t = 2 and so on, some very interesting patterns and behaviors begin to emerge.

These are the automata of the modern day.

But Leibniz had an even grander, further reaching idea in mind in his The Monadology. He wasn’t just crafting a colorful game; he was building an entire universe.

Leibniz called his particular version of automata monads. And whereas thinkers like René Descartes had cleaved apart the mental and the physical, Leibniz’s monads gave him a way to fuse these two pieces—mind and body—into a unified whole.

The crux of Leibniz’s approach to mind and body centers on a counterargument he posed to Descartes. The latter had supposed that the defining feature of the physical world is its properties of extension and motion. Descartes felt certain that the mental and the physical were separate substances, because the latter possessed these two properties and the former didn’t. But Leibniz had a rebuttal:

The nature of body does not consist merely in extension, that is, in size, shape, and motion, but we must necessarily recognize in body something akin to souls, something we commonly call substantial form, even though it makes no change in the phenomena, any more than do the souls of animals, if they have any.

Gottfried Wilhelm Leibniz

And, of course, Leibniz had some very well-reasoned points to back this assertion up (he was what we call a “rationalist” after all, one who believes in the supremacy of reason!).

Leibniz had two main arguments directed towards Descartes’ assertion that matter can be identified with extension and motion. First, he argued that if there were nothing in the physical except size and shape, physical bodies (the objects we see around us) would offer no resistance to each other. A rolling pebble could crash into a stationary boulder without losing an ounce of its own force. Second, if matter were merely extension, we could never actually come to identify individual bodies, because extension is infinitely divisible. At whatever point we stop dividing, we still meet an aggregate, an extensible group of matter.

Therefore—every portion of matter in the universe must be coupled with an indivisible, incorporeal unified substance. Every bit of reality is fundamentally a monad. And each of these monads is a mind, a mental force which, in perceiving various things, generates the seemingly physical world.

Notice that this is an even more sophisticated view on automata than seen in John Conway’s Game of Life. In the Game of Life, we have squares and grids like so:

Each of these cells and their states is an externalized projection. States rest upon the background space that is the grid of cells.

But Leibniz’s monads are something else entirely.

Leibniz’s monads contain each of their states within themselves. In Leibniz’s model of the universe, there is nothing which is truly external to anything else.

The automata that is a monad might therefore be rendered like this:

Leibniz also called these monads “Entelechies,” from the Greek entelecheia meaning roughly “to have completion.”

In section 18 of his The Monadology, Leibniz claims that these monads “have in them a certain perfection; they have a certain self-sufficiency which makes them the sources of their internal activities and, so to speak, incorporeal automata.”

Those supposedly two, distinct substances that Descartes spoke so fondly of—mind and body—are fused in Leibniz’s monads. As Leibniz himself words it, “the Monad […] is nothing but a simple substance, which enters into compounds. By ‘simple’ is meant ‘without parts.’” 

To round things out, Leibniz argued that a sort of Ultimate Monad or Divine Figure gave rise to each of the infinite monads of the universe. Leibniz’s rationale for this idea consisted of three core points (taken from The Monadology itself):

1. No dissolution of these elements need be feared, and there is no conceivable way in which a simple substance can be destroyed by natural means.
2. For the same reason there is no conceivable way in which a simple substance can come into being by natural means, since it cannot be formed by the combination of parts [composition].
3. Thus it may be said that a Monad can only come into being or come to an end all at once; that is to say, it can come into being only by creation and come to an end only by annihilation, while that which is compound comes into being or comes to an end by parts.

Thus, God alone is the primary unity or original simple substance, of which all created or derivative Monads are products and have their birth, so to speak, through continual fulgurations of the Divinity from moment to moment, limited by the receptivity of the created being, of whose essence it is to have limits.

Leibniz’s God, however, was a much different one than the God of the Bible or the God of his time’s religious atmosphere.

This was a creator who was distributed throughout the whole universe. This was a creator who was intimately connected to each entity of reality. This was a monistic God, and there could be no true separation between creator and created.

Dare we say, Leibniz’s monistic God made Descartes’ dualistic God seem a bit more like the latter’s “evil demon”…

Now, with our deep dive into rationalism fully complete, we can turn to the world of empiricism. And, to keep with a major theme of this article, we’ve got yet another circle to see. Onwards to the Vienna Circle.

Logical Empiricism and the Vienna Circle

Despite the name, the Vienna Circle wasn’t exactly a circle. It was more of a hodgepodge of assorted early-20^th-century Austrian geniuses who met at the local coffeeshop to talk philosophy:

Oh yeah… and we can’t forget this devil either:

Although there were right around a dozen or more people associated with the Vienna Circle, we’ll set our sights on some of the two loudest and proudest (and quite possibly the most gifted) of the bunch—Ludwig Wittgenstein and Rudolf Carnap. 

Wittgenstein is somewhat of a household name, even amongst people who aren’t big on philosophy. Many people know of him from his rabbit-duck metaphor:

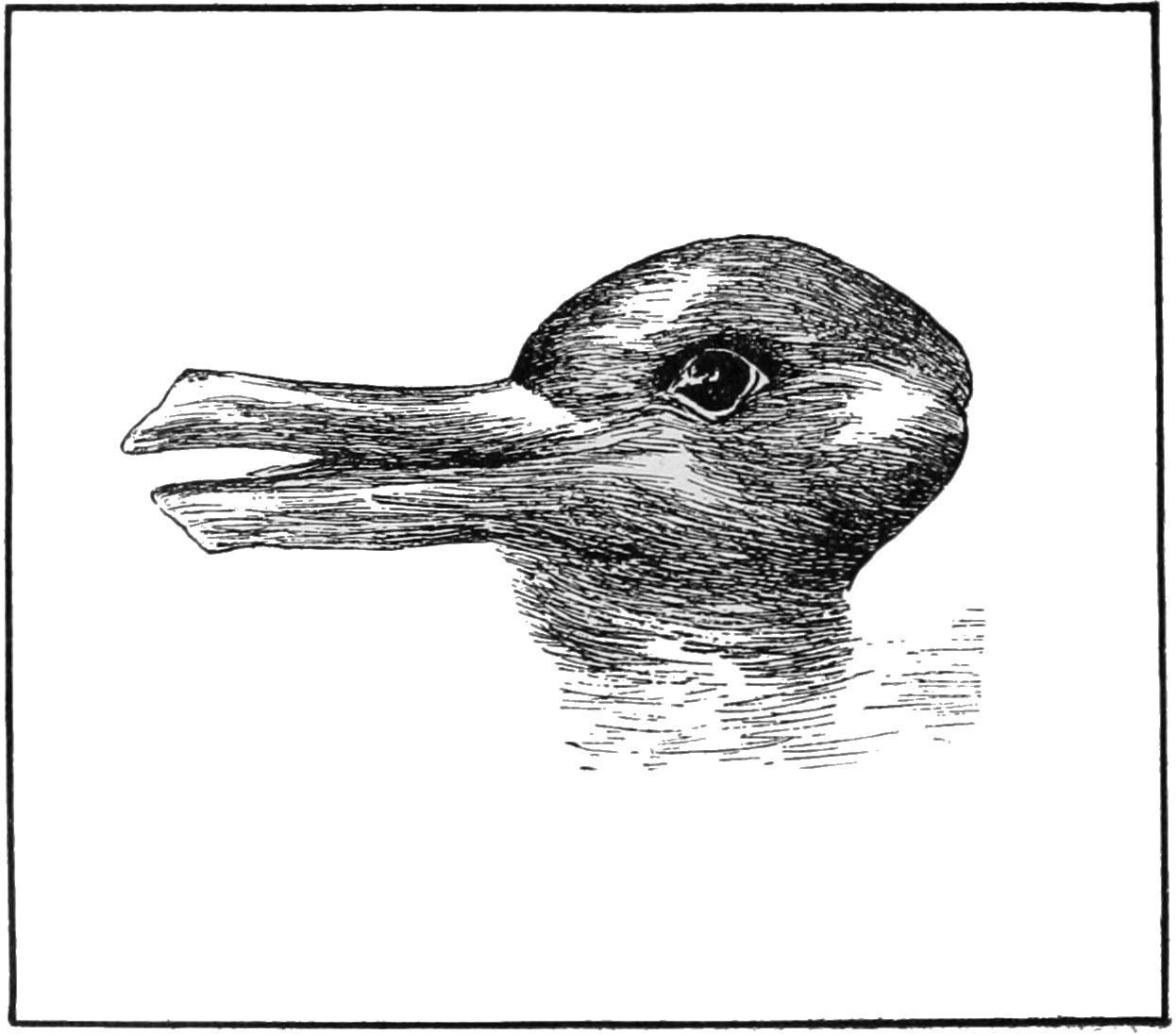
But this was from a Wittgenstein of a later age, a Wittgenstein who had moved far beyond the Vienna Circle and its core themes and beliefs. 

Funnily enough, the Wittgenstein of the 1920s and 1930s was technically not even a member of the Vienna Circle. The circle’s leader, Moritz Schlick, happened across his 1921 book Tractatus Logico-Philosophicus and was so impressed that he invited Wittgenstein to join the group. However, Wittgenstein—somewhat of a recluse and often extremely defensive of and sensitive about his ideas—never took him up on the offer.

Nonetheless, Wittgenstein’s Tractatus left such a mark on Schlick that he introduced and recommended the book to the rest of the Vienna Circle. Schlick even told Albert Einstein that Wittgenstein’s book was the “deepest” work of “the new philosophy” that the Vienna Circle had come to advocate for.

But what exactly was this “new philosophy?”

To get as good of a grip on the Vienna Circle and this new philosophy of theirs, we should briefly drop back in on our friends Plato and Aristotle and their view of the universe. 

Plato’s answer to the question, “What makes a circle a circle?”, and for that matter “What makes anything anything?” was to assume an ideal world, a world above and beyond both the perceivable world around us and the world of our thoughts, feelings and imaginations. A circle is a circle because it is given this “circleness” by the ideal form of a circle, residing in an otherworldly realm: 

And this otherworldly realm was somehow connected to both our minds and the world around us: 

But Plato’s protégé, Aristotle, wasn’t too keen on this approach. Aristotle made up his mind that there is no such “otherworldly realm” and that whatever “forms” are, they cannot exist in a completely separate section of reality. Aristotle sought to simplify things. He sought to examine the precise relationships to be found between body and mind, concrete and abstract:

And conducted these examinations largely through a brand new tool of science he invented—logic. This is one and the same tool that Wittgenstein and the Vienna Circle was so interested in. Only this time—over two thousand years later—logic looked a bit different.

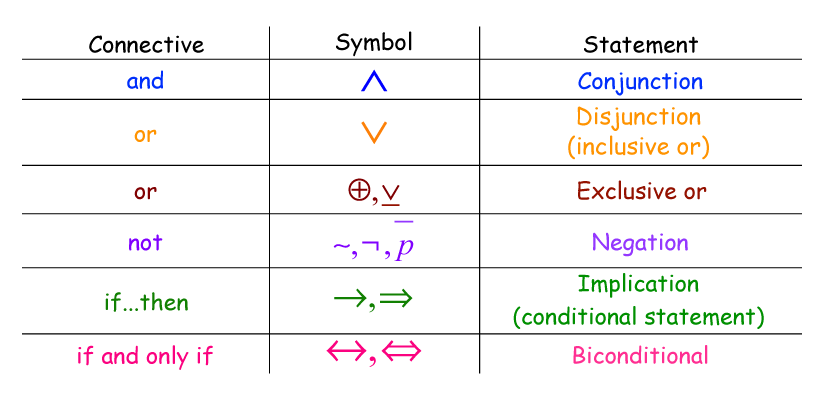
Wittgenstein and company were focused on what are called logical propositions. Logical propositions consist of certain “statements” or propositions which are connected by a certain arrangement of “logical connectives.” Aristotle had the “statements” but he did not yet have many of the “logical connectives” that the Vienna Circle had at their disposal. Aristotle worked primarily with “NOT” or the negation of statements. Wittgenstein and company had these to work with:

Wittgenstein and his contemporaries also had a more precise version of what Aristotle referred to as the “universal” and “particular” forms of statements. Philosophers of the early 20^th century had something called predicate logic at their disposal, something which made the universal and the particular forms of statement much easier to use and far more specific in nature:

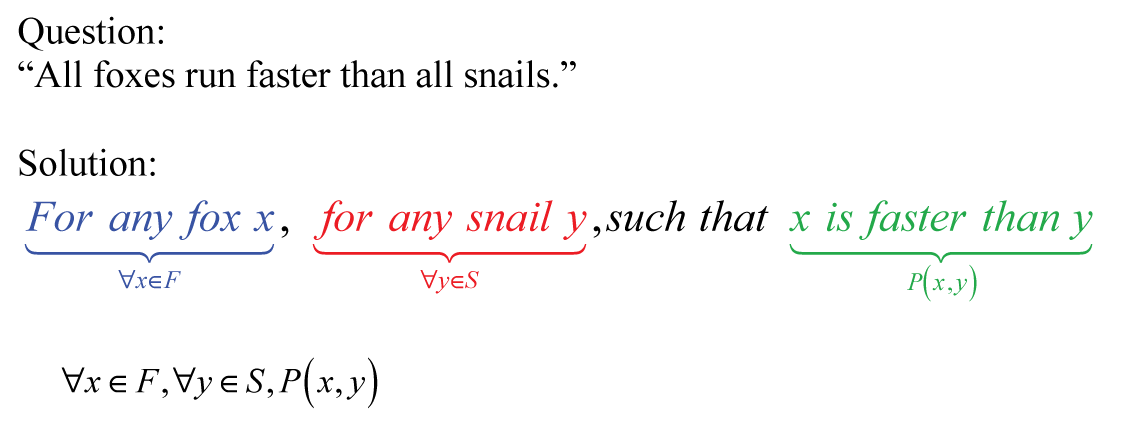
With these fancy new tools in hand, many philosophers got a bit carried away. Could it be that the entirety of reality could be reduced to that which can be analyzed through logical structure?

Wittgenstein, admittedly, took more of a nuanced approach to this grand reduction. The crux of his Tractatus Logico-Philosophicus is something known as the “picture theory” of meaning. The most straightforward way to understand this approach is to understand these two graphics: 

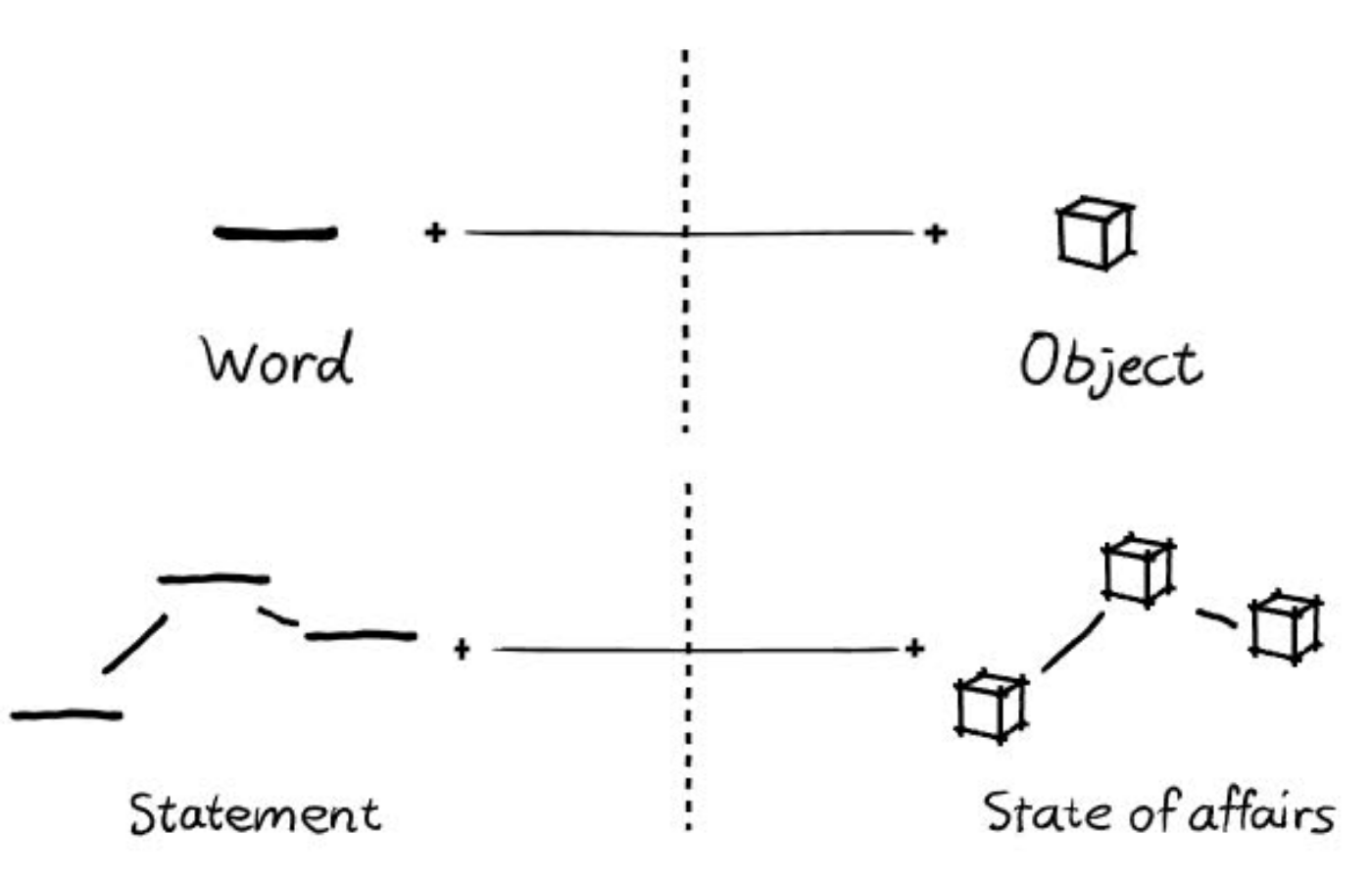
Wittgenstein held that the job of logical statements (like the ones seen above) is to mirror the world, or the “state of affairs” and constituent “objects” that they have in them. 

But a bit of a problem arose when one moved from speaking of states of affairs of the world to more vague notions related to ethics, spirituality or metaphysics (the study of reality at large).

Wittgenstein took language (or logical statements) to be the limit of reality. In other words, although one could use language to investigate or “picture” the world, one could not self-referentially use language upon its own structure. Thus, the truly metaphysical, the study of those logical statements themselves, we could not even speak of. We could not so much as bring language in conformance with this portion of reality. This is where his infamous, “Whereof one cannot speak, thereof one must be silent,” derives its meaning from.

Also on this topic, Wittgenstein made a metaphor between the vision of the eye and the nature of metaphysics. In proposition 5.6331, he claims “For the field of sight has not a form like this:”

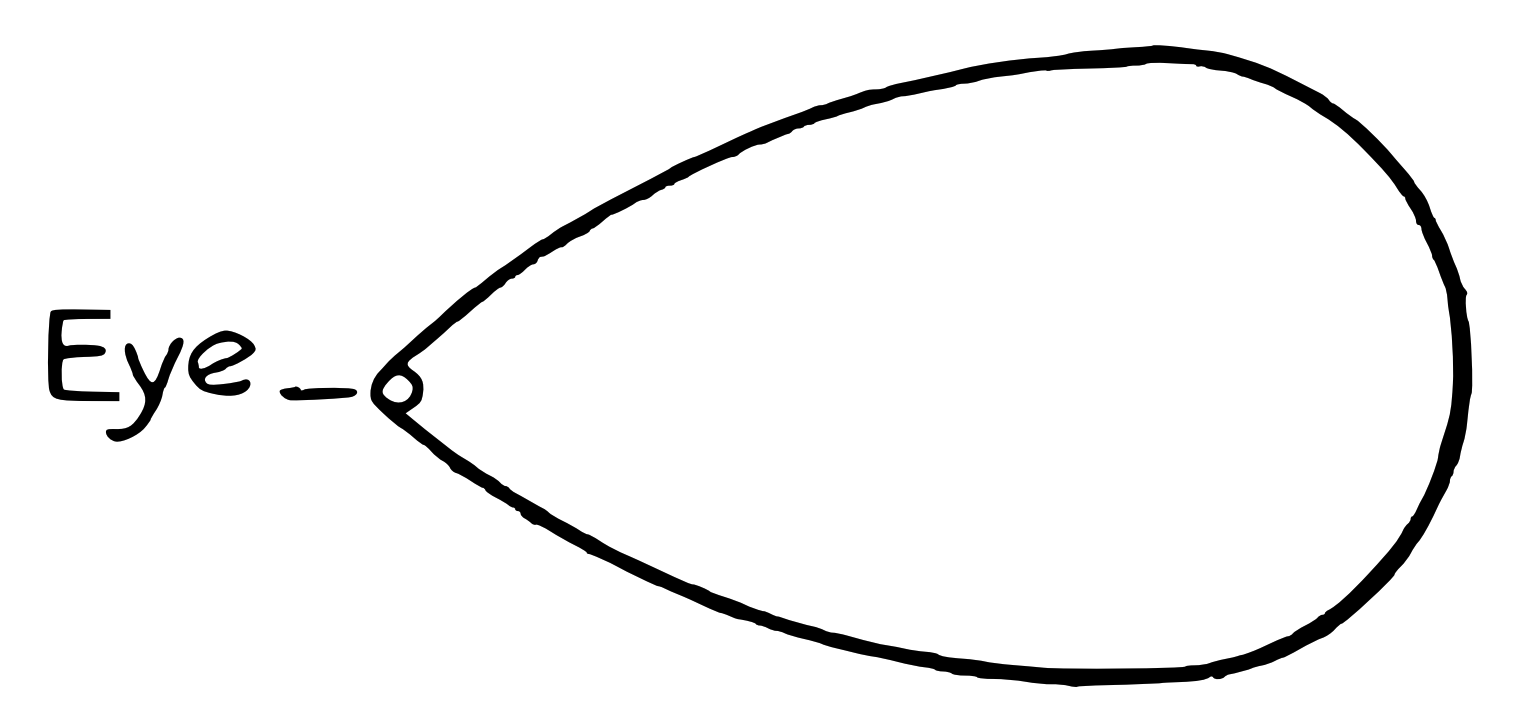
He says:

Where in the world is a metaphysical subject to be noted? You say that this case is altogether like that of an eye and a field of sight. But you do not really see the eye. And from nothing in the field of sight can it be concluded that it is seen from an eye. 

Ludwig Wittgenstein

So… if there is no discernible “I” in the visual field of reality, so to speak, how do mind and body relate to one another? Was the Wittgenstein of the Tractatus a dualist or a monist? Or, perhaps, was he something else entirely?

This is a subtle issue. What is often called “the early Wittgenstein” and his contemporaries in the Vienna Circle attempted to sidestep what we’ve called “the battle between body and mind.” 

The Vienna Circle experimented with something called logical empiricism. This was a brand new approach, the gist of which is best explained by Rudolf Carnap in his 1935 book Philosophy and Logical Syntax:

From the Monists we learn: “There is only one principle on which all that is, is founded”; but the Dualists tell us: “There are two principles”. The Materialists say: “All that is, is in its essence material”, but the Spiritualists say: “All that is, is spiritual”. […] Now let us examine this kind of proposition from the point of view of verifiability. It is easy to realize that such propositions are not verifiable. From the proposition: “The Principle of the world is Water” we are not able to deduce any proposition asserting any perceptions or feelings or experiences whatever which may be expected for the future. Therefore the proposition, “The Principle of the world is Water”, asserts nothing at all. 

Rudolf Carnap

This was the bedrock of the logical empiricists—metaphysical statements mean nothing at all. Only our experience of the world and logical inference based upon those experiences can tell us anything at all. 

In this sense, our Vienna Circle friends might be described as sorts of “nondualists.” Although they certainly weren’t nondualists in the usual, spiritual sense, they rejected the dichotomy between mind and body completely. They did not even accept the question, “What substance is reality made of?” as a valid inquiry.

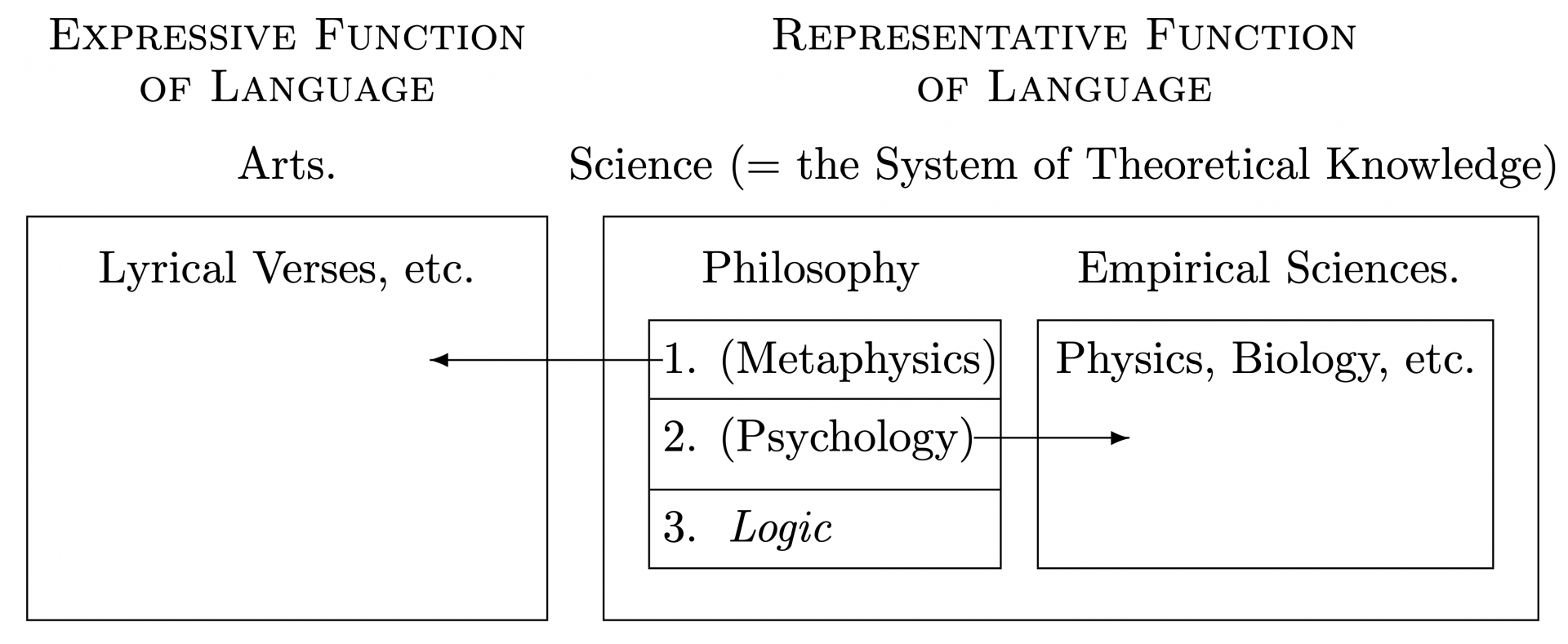
In essence, those of the Circle admitted that his is a helpful way of looking at things:

But they thought it only a mere convenience that we consider each half of the “mind ⟷ body” equation to be a substance. Whatever we could know about each half, we could never delimit its entire, “metaphysical” nature. All we could hope to do is gather data from the left and reason about it on the right. It was a very cut-and-dried, mechanical view of the world.

Rudolf Carnap goes on the attack against metaphysics in is entirety in his Philosophy and Logical Syntax, asserting:

Metaphysicians cannot avoid making their propositions non-verifiable, because if they made them verifiable, the decision about the truth or falsehood of their doctrines would depend upon experience and therefore belong to the region of empirical science. This consequence they wish to avoid, because they pretend to teach knowledge which is of a higher level than that of empirical science. Thus they are compelled to cut all connection between their propositions and experience; and precisely by this procedure they deprive them of any sense.

Rudolf Carnap

Much as Wittgenstein asserted that “Whereof one cannot speak, thereof one must be silent,” Carnap asserted that metaphysical statements could, technically, “be spoken of” but that they didn’t really have any content; they didn’t represent anything.

This attitude of Carnap’s is apparent in one of his graphics from Philosophy and Logical Syntax:

Carnap went on to attempt a brute reduction of philosophy—the only proper task of philosophy, he asserted, is logical analysis.

Yet, as streamlined and focused as Carnap’s approach was, come the second half of the 20^th century, the logical empiricism of the Vienna Circle began to lose its appeal.

Perhaps one of the biggest impediments to logical empiricism’s popularity was the character of a man—Thomas Kuhn. Many people have heard of Kuhn in conjunction with his notion of the “paradigm shift,” (which wasn’t actually coined by him, by the way) but there is something even closer to Kuhn’s heart that changes the way we look at reality—the so-called theory-dependence of scientific observation and the impact that scientists’ internal worlds have on the observations they make of the world.

Next and final stop, Thomas Kuhn and the latest paradigm in the study of mind, body and reality—dual-aspect monism.

Dual-Aspect Monism: Marrying Mind with Matter for Good?

The Vienna Circle and the rest of the logical empiricists had their fun, but come the 1960s and 1970s, there was not much left of them. In 1961 Thomas Kuhn published his The Structure of Scientific Revolutions and the content of this still-popular work casts some serious shadows on the logical empiricists’ way of thinking.

To simplify a great deal, Kuhn’s core argument against logical empiricism attacked one of the deepest assumptions of the movement—that observations of the world are somehow “objective” and unaffected by the theoretical or mental structure of the scientists themselves. 

Perhaps the easiest way to understand what Kuhn was getting at is through the following graphic: 

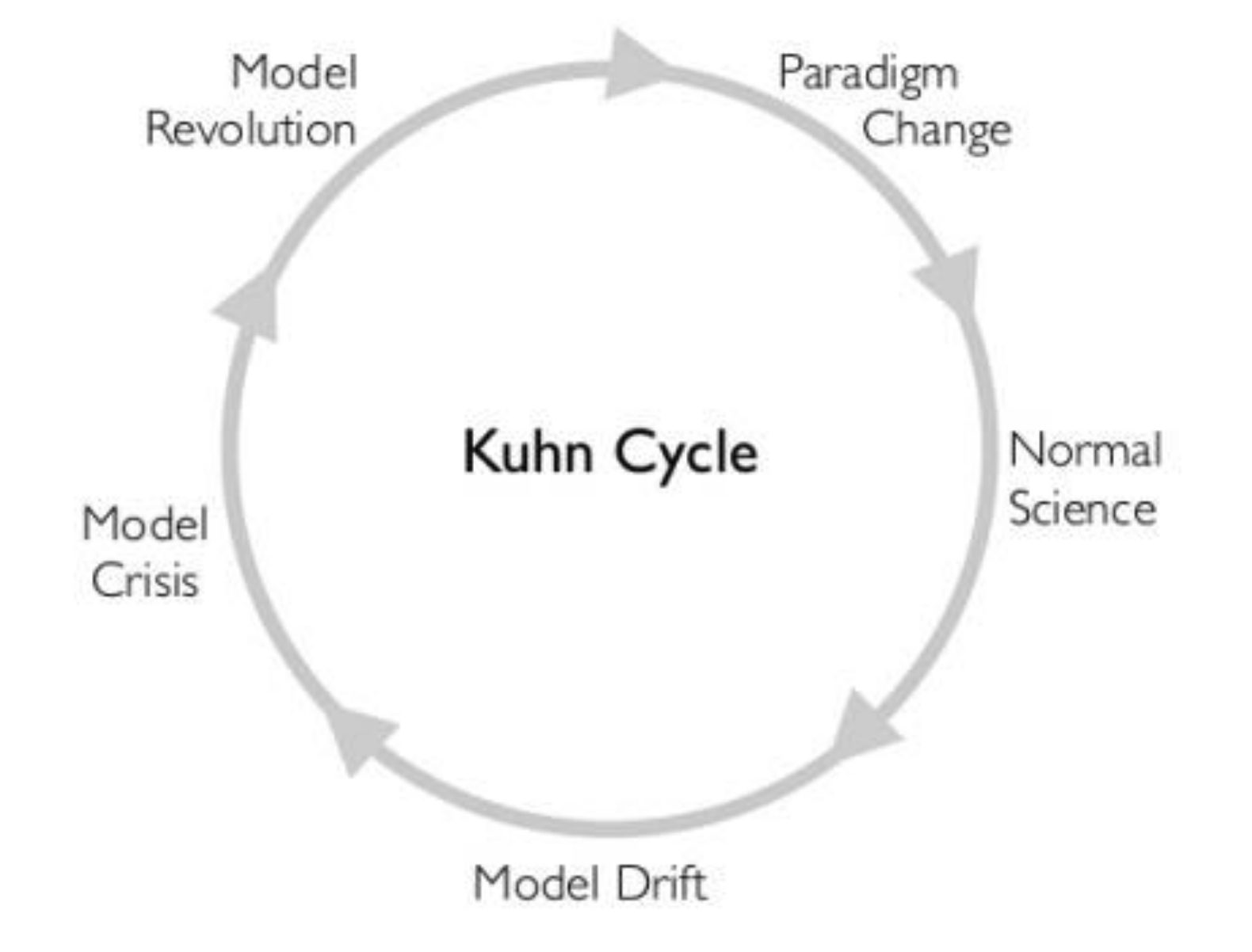
At any given era of scientific thought, scientists operate within a given “model” of how the world works. We might view this model as the assumptions or “axioms” beneath the theories that the scientists create about the world.

Before Einstein’s relativity theories and before Carl Friedrich Gauss and Bernhard Riemann’s “non-Euclidean” geometries, it was assumed that the geometry of the universe adhered to Euclid’s postulates (axioms). But once this assumption was countered, the entire model of scientific observation was altered. This expanded the “reach” of scientific theories, stripping away some of the previous constraints on what could be observed.

This is reflected in “Kuhn’s Cycle” above.

Under any set of scientific assumptions or un-questioned axioms of the era, there is “Normal Science.” But, as observations of the world accumulate and new processes are seen, oftentimes these assumptions start to “drift.” It is this “Model Drift” that eventually spawns radically different axiom sets or patterns of assumption. And the difference between the theories spawned by these different assumptions will, for all intents and purposes, be what Kuhn calls “incommensurable.” In other words, there will be no objective theoretical ground upon which to evaluate both of these theories against one another. It is a scientific stalemate.

This is the “Model Crisis” above.

The only viable way to resolve such a “model crisis” is to extend the current set of axioms or assumptions in use by the scientific community. These axioms must be extended to accommodate both sides of the “drifted models.” There must be a unification.

This unification is put into action by what Kuhn terms a “Model Revolution.” New concepts and new axioms are generated that can abstract over all previous axioms, such that no paradoxes or incompatibilities remain.

And, once this revolution is complete, all future observations—until the next big change that is!—will be interpreted under the new set of assumptions or axioms. This is the completion of the “Paradigm Change.”

From Kuhn we see that all truly is in flux. It is not simply that the world around us is changing against some sort of “fixed background” of concepts or some sort of objective measuring tape. In some sense, the world changes around us, according to our own assumptions about it.

But, of course, we have to be very careful about this… How exactly does this work? And what does this mean for our old friends, dualism and monism?

Thankfully, the decades following Kuhn’s The Structure of Scientific Revolutions helped to answer these questions. And, fascinatingly enough, the explorations of the mind—psychedelics and consciousness expansion galore—and the wild personal experimentations that came with the 70s helped much more than we may ever know.

This book cover might explain things best.

Yes, in some sense the hippies really did save physics (and metaphysics!). But how did they do it?

It all comes down to one idea—perhaps observation and consciousness are essential to reality. 

Contra the hyper-division of Descartes’ dualism, what if body and mind are simply opposite sides of one and the same coin? Enter dual-aspect monism.

Perhaps the most prominent proponent of dual-aspect monism was the physicist John Archibald Wheeler. In 1979 Wheeler not only coined the ubiquitous phrase “black hole,” but he also set out to discover the deep nature of reality in his 1980 article, “Beyond the Black Hole.” In this article, Wheeler focused on one core notion, something he called the participatory universe.

This “participatory universe” builds on something known as the anthropic principle.

The anthropic principle arose in 1957 when physicists were obsessed with the so-called fine-tuning problem—the fundamental constants and quantities of the inception of our universe fall into such an incredibly precise range that, if it were not so precise, intelligent observers never could have existed; why is this the case?

In other words, it seems that the entire universe conspired to create intelligent observers, at least from a statistical perspective. How can this be?

Physicist Robert H. Dicke’s answer to this question was a matter-of-fact one. His “anthropic principle” states that the question of “why” the universe is finely tuned for life is not so much of an interesting question at all. The very fact that there are intelligent observers like us means that, obviously, there would appear to be such fine-tuning.

But to many, this was a non-sequitur. To John Wheeler, this answer wasn’t much of an answer at all. Wheeler set out to develop something even stronger, something he called the participatory principle: 

Stronger than the Anthropic Principle is what I might call the Participatory Principle. According to it, we could not even imagine a universe that did not somewhere and for some stretch of time contain observers, because the very building materials of the universe are these acts of observer-participancy. … This participatory principle takes for its foundation the absolutely central point of the quantum: no elementary phenomenon is a phenomenon until it is an observed (or registered) phenomenon.

John Wheeler

Wheeler included an inspiring visual of such a universe, an eye gazing upon itself. Here’s an adapted version of the original: 

This is what’s called a “dual-aspect monism.” And in this view, both body and mind are self-generating and mutually reinforcing aspects of reality. It’s a symbiosis of form, and there is something admittedly quite elegant about it. 

Plato sought to explain body and mind through a third, “ideal” world. Aristotle sought to exhaustively delimit the structure of the interactions between body and mind. Descartes tried to correlate body and mind, all while separating them into two supposedly “immiscible” substances. Leibniz tried to explain all matter in terms of mind.

But with Wheeler and his notion of a participatory universe, we come “full circle” to those before Plato and company. We are back at a somewhat mystical, spiritual integration of mind and body. And we’re given the exciting vision—perhaps us humans aren’t as supposedly insignificant as science used to assume we are. 

Perhaps with this participatory vision of our minds and bodies—of our shared reality—we are one step closer to gazing up at the night sky and finally knowing “why?”: